The persistent Laplacian of non-branching complexes
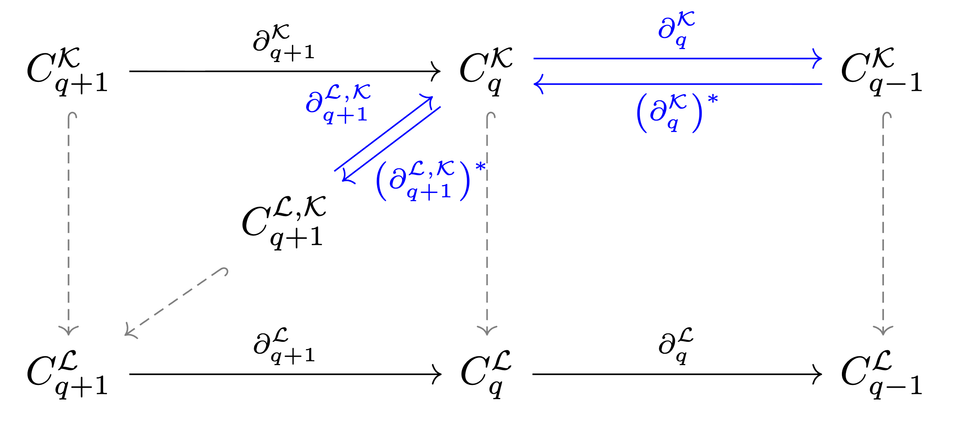
This recently published paper by CTA2 members Magnus Bakke Botnan and Rui Dong studies persistent Laplacians, an extension of Laplacian methods from graph theory to higher-dimensional topological structures. The authors show that for non-branching complexes (such as pseudomanifolds), these operators can be computed efficiently in a given dimension, making spectral methods feasible for certain large geometric and image-based data sets. Connections are also made to the spectral properties of hypergraphs.
Published version:
The persistent Laplacian of non-branching complexes
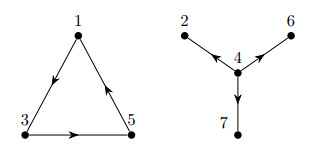
Non-branching matrices are real matrices with entries in $ \{-1, 0, 1\} $, where each row contains at most two non-zero entries. Such matrices naturally arise in the study of Laplacians of pseudomanifolds and cubical complexes. We show that a basis for the kernel of a non-branching matrix can be computed in near-linear time. Specifically, the basis has the special property that the supports of all the column vectors in it are disjoint with each other. Building on this result, we show that the up persistent Laplacian can be computed in near-linear time for a pair of such spaces, and its eigenvalues can be more efficiently computed via computing singular values. In addition to that, we analyze the arithmetic operations of up persistent Laplacian with respect to a non-branching filtration. Furthermore, we show that the up persistent Laplacian of $ q $-non-branching simplicial complexes can be represented as the Laplacian of an associated hypergraph, thus providing a higher-dimensional generalization of the Kron reduction, as well as a Cheeger-type inequality. Finally, we highlight the efficiency of our method on image data.
Arxiv version:
The persistent Laplacian of non-branching complexes
Non-branching matrices are real matrices with entries in $\{-1,0,1\}$, where each row contains at most two non-zero entries. Such matrices naturally arise in the study of Laplacians of pseudomanifolds and cubical complexes. We show that a basis for the kernel of a non-branching matrix can be computed in near-linear time. Especially, the basis has the special property that the supports of all the column vectors in it are disjoint with each other. Building on this result, we show that the up persistent Laplacian can be computed in near-linear time for a pair of such spaces and its eigenvalues can be more efficiently computed via computing singular values. In addition to that, we analyze the arithmetic operations of up persistent Laplacian with respect to a non-branching filtration. Furthermore, we show that the up persistent Laplacian of $q$-non-branching simplicial complexes can be represented as the Laplacian of an associated hypergraph, thus providing a higher-dimensional generalization of the Kron reduction, as well as a Cheeger-type inequality. Finally, we highlight the efficiency of our method on image data.


