The Hopf-Rinow theorem and the Mañé critical value for magnetic geodesics on odd-dimensionl spheres
Peter Albers, Gabriele Benedetti, and Levin Maier
Abstract
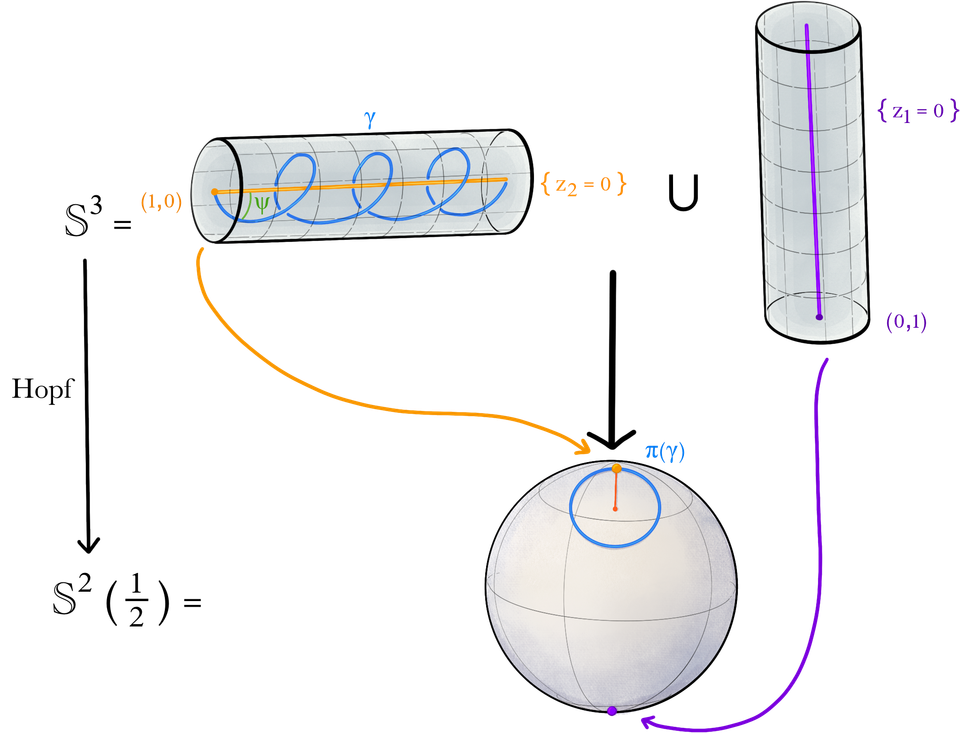
The subject of this article are magnetic geodesics on odd-dimensional spheres endowed with the round metric and with the magnetic potential given by the standard contact form. We compute the Mañé critical value of the system and show that a value of the energy is supercritical if and only if all pairs of points on the sphere can be connected by a magnetic geodesic with that value of the energy. Our methods are explicit and rely on the description of the submanifolds invariant by the flow and of the symmetries of the system, which we define for a general magnetic system and call totally magnetic submanifolds and magnetomorphisms, respectively. We recover hereby the known fact that the system is super-integrable: the three-spheres obtained intersecting the ambient space with a complex plane are totally magnetic and each magnetic geodesic is tangent to a two-dimensional Clifford torus. In our study the integral of motion given by the angle between magnetic geodesics and the Reeb vector field plays a special role, and can be used to realize the magnetic flow as an interpolation between the sub-Riemannian geodesic flow of the contact distribution and the Reeb flow of the contact form.