Extremal Betti Numbers and Persistence in Flag Complexes

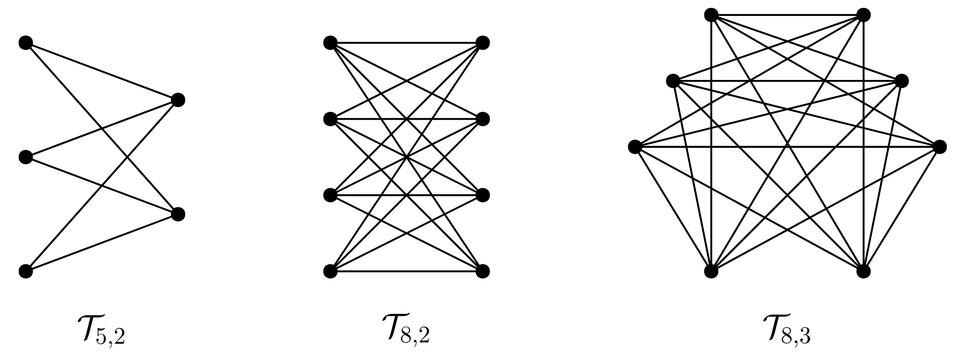
We investigate several problems concerning extremal Betti numbers and persistence in filtrations of flag complexes. For graphs on $n$ vertices, we show that $β_k(X(G))$ is maximal when $G=\mathcal{T}_{n,k+1}$, the Turán graph on $k+1$ partition classes, where $X(G)$ denotes the flag complex of $G$. Building on this, we construct an edgewise (one edge at a time) filtration $\mathcal{G}=G_1\subseteq \cdots \subseteq \mathcal{T}_{n,k+1}$ for which $β_k(X(G_i))$ is maximal for all graphs on $n$ vertices and $i$ edges. Moreover, the persistence barcode $\mathcal{B}_k(X(G))$ achieves a maximal number of intervals, and total persistence, among all edgewise filtrations with $|E(\mathcal{T}_{n,k+1})|$ edges. For $k=1$, we consider edgewise filtrations of the complete graph $K_n$. We show that the maximal number of intervals in the persistence barcode is obtained precisely when $G_{\lceil n/2\rceil \cdot \lfloor n/2 \rfloor}=\mathcal{T}_{n,2}$. Among such filtrations, we characterize those achieving maximal total persistence. We further show that no filtration can optimize $β_1(X(G_i))$ for all $i$, and conjecture that our filtrations maximize the total persistence over all edgewise filtrations of $K_n$.