Cobordism of nested manifolds

By Alba Sendón Blanco

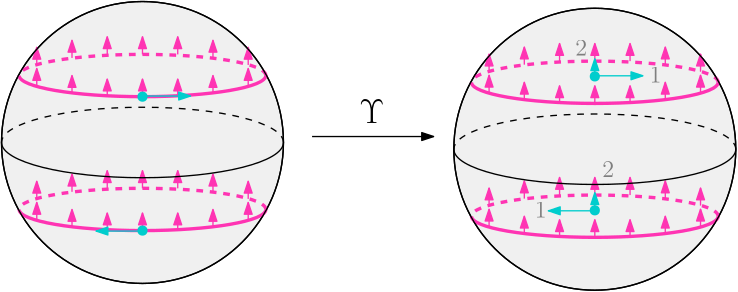
Imagine that you have a nested manifold: a small manifold inside a big manifold. You know that the big manifold is a boundary and that the small manifold is a boundary. With this information, when can you assert that your nested manifold is a nested boundary?Wall already knew that stably, the answer to this question is "always". This document delves further in this problem via a nested Pontryagin-Thom construction: the study of nested manifolds up to cobordism amounts to the study of the homotopy groups of... bananas! As a consequence, we give an alternative proof of Wall's result. Moreover, we conclude that the unstable answer to the above question is "not always". Particularly, when our big manifold has a trivial normal direction, we can move the small manifold apart from the big manifold along this direction (as in the picture), hence turning our nested manifold into two disjoint manifolds, i.e. a link. This gives interesting nested cobordism invariants coming from cobordism invariants for links.

See the full preprint below

Cobordism of nested manifolds

We study cobordisms of nested manifolds, which are manifolds together with embedded submanifolds, which can themselves have embedded submanifolds, etc. We identify a nested analog of the Pontryagin-Thom construction. Moreover, when the highest-dimensional manifold has a normal bundle with a framed direction, we find spaces homotopy equivalent to the nested Pontryagin-Thom spaces that relate nested manifolds up to cobordism with links up to cobordism. This gives rise to nested cobordism invariants coming from previously studied cobordism invariants of links. In addition, we provide an alternative proof of a result by Wall about the splitting of the stable nested cobordism groups.

arXiv.orgAlba Sendón Blanco